Трапеция
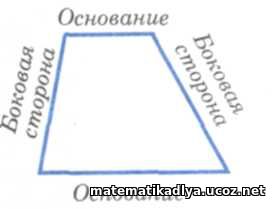
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
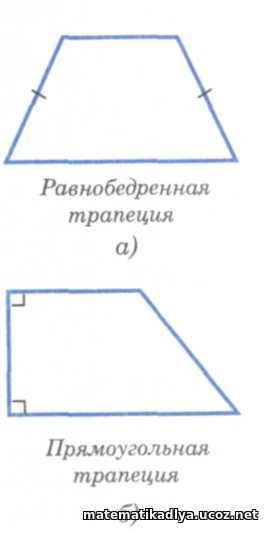
Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
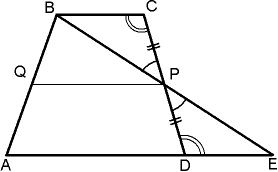
Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Пусть ABCD – данная трапеция.EF – средняя линия трапеции. Проведем через вершину B и точку F прямую. Пусть эта прямая пересекает прямую AD в некоторой точке G.
Δ CFB = Δ FDG по второму признаку равенства треугольников (CF = FD, по построению, <BCF = <EВА, как внутренние накрест лежащие при параллельных прямых ВС и DG и секущей CD, <CFB = <DFG, как вертикальные). Значит BC = DG и BF = FG.
Поэтому, средняя линия трапеции EF является средней линией треугольника ABG. По свойству средней линии треугольника EF || AD, а
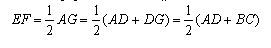
Теорема доказана.
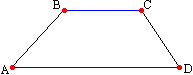
Определение 1. Трапецией называется четырехугольник, у которого одна пара параллельных сторон.
Определение 2. Основаниями трапеции называют её параллельные стороны.
Определение 3. Боковыми сторонами трапеции называют её непараллельные стороны.
Параллельные стороны не могут быть равными, т.к. в противном случае мы имели бы параллелограмм. Поэтому одну из них мы назовем большим, вторую - малым основанием трапеции. Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить "особый вид" высот.
Определение 4. Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
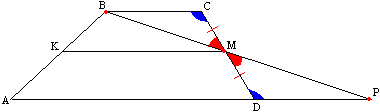
Теорема 2. Средняя линия трапеции параллельна основаниям и равна их полусумме.
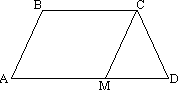
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, РВСМ=РМDР - накрестлежащие, РВМС=РDМР - вертикальные), поэтому ВМ=МР или точка М - середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
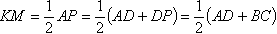
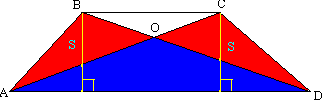
Теорема 3. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равновелики.
Напомним, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
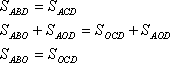
Теорема 4. В трапеции середины оснований и точка пересечения диагоналей лежат на одной прямой.
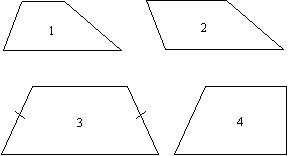
Виды трапеций:
Определение 5. (рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 6. (рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 7. (рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 8. (рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 5. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ. Она пересечет большое основание в точке М. Четырехугольник АВСМ является параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD - равнобедренный, РСМD=РСDM, и, значит, РА=РD. Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
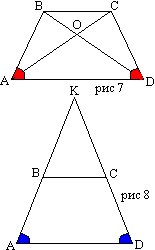
Теорема 6. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 7. Если продолжить стороны равнобочной трапеции до их пересечения, то вместе с большим основанием трапеции они образуют равнобедренный треугольник.
Доказательство. По теореме углы А и D равны. Поэтому треугольник АDК является равнобедренным по признаку: если в треугольнике два угла равны, то он равнобедренный.
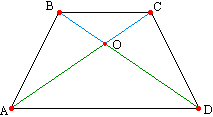
Теорема 8. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому РОАD=РОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 10. Осью симметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 9. Ось симметрии равнобокой трапеции перпендикулярна её основаниям.
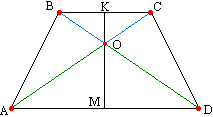
Вспомним свойство равнобедренного треугольника: медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника. Вследствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 10. Если углы, прилежащие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 11. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 12. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 13. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 14. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник).
Теорема 15. Радиус вписанной в трапецию окружности равен половине высоты основания.
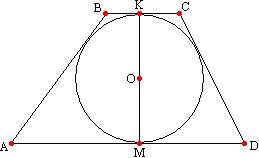
Доказательство этой теоремы заключается в объяснении того, что радиусы проведенные к основаниям лежат на высоте трапеции. Из точки О - центра вписанной в данную трапецию АВСD окружности проведем радиусы в точки касания её основаниями трапеции. Как известно, ридиус, проведенный в точку касания, перпендикулярен касательной, поэтому ОК^ВС и ОМ^AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общий перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 16. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.

Доказательство: Пусть ABCD - данная трапеция, а AB и CD - её основания. Пусть также AH - высота, опущенная из точки A на прямую CD. Тогда S ABCD= SACD + SABC. Но SACD = ½AH·CD, а SABC = ½AH·AB. Следовательно, SABCD = ½AH·(AB + CD). Что и требовалось доказать.
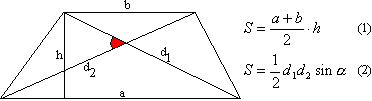
Вторая формула перешла от четырехугольника.