Правильный пятиугольник

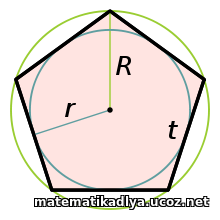
Правилый пятиугольник

 

Правильный пятиугольник или пентагон — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Построение правильного пятиугольника

У правильного пятиугольника угол равен

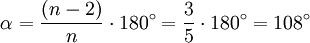
Площадь правильного пятиугольника с длиной стороны t рассчитывается по формуле:

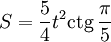
или
,
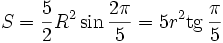где R — радиус описанной окружности, r — радиус вписанной окружности.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу.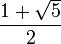
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
Сторона правильного пятиугольника:

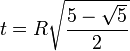
Высота правильного пятиугольника:

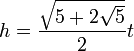
Площадь правильного пятиугольника:

Радиус вписанной окружности правильного пятиугольника:

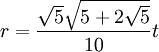
Радиус описанной окружности правильного пятиугольника:

Пятиугольником невозможно заполнить плоскость без промежутков.

Построение

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
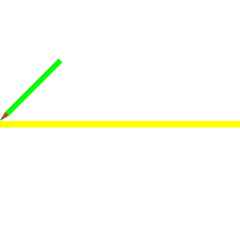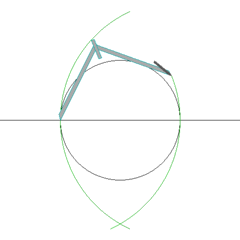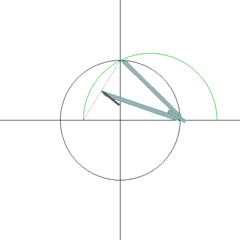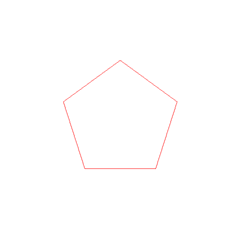
Вот один из методов построения правильного пятиугольника в заданной окружности:

By Aldoaldoz - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10023658

 

1. Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

 

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Правильный шестиугольник

 

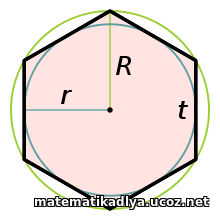
Правильный шестиугольник

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Свойства

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности .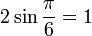
Все углы равны 120^°.
Радиус вписанной окружности равен:

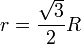
Периметр правильного шестиугольника равен:

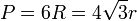
Площадь правильного шестиугольника рассчитывается по формулам:


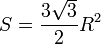
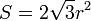
Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
Правильный шестиугольник со стороной 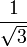является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной 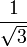(лемма Пала).

Построение

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

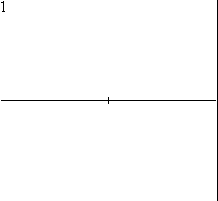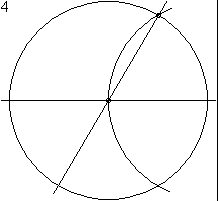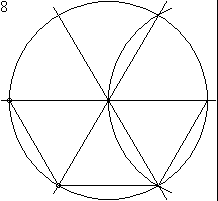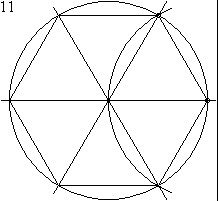
Правильный семиугольник

 

Правильный семиугольник

Правильный семиугольник — это правильный многоугольник с семью сторонами.

Свойства

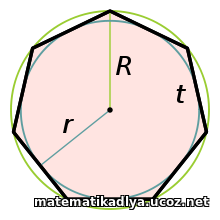
Пусть t — сторона семиугольника, R — радиус описанной окружности, r — радиус вписанной окружности.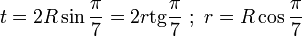
Периметр правильного семиугольника равен

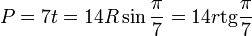
Площадь правильного семиугольника рассчитывается по формулам:




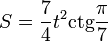
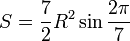
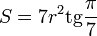
Построение

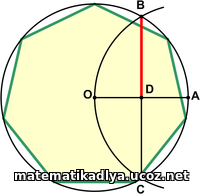
Приближённое построение правильного семиугольника

Точное

Согласно теореме Гаусса — Ванцеля, правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и размеченной линейки то есть линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).

Приближённое

Приближённое (но с достаточной для практики точностью - 0,2 %) построение семиугольника показано на рисунке. Из точки A на окружности радиусом, равным радиусу окружности, проводим дугу BOC. Отрезок 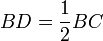и даст искомое приближение.

Семиугольные звезды

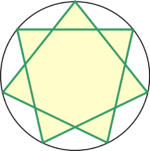
Семиугольная звезда 7/2

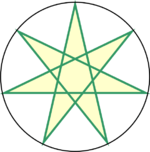
Семиугольная звезда 7/3

Существует два звёздчатых семиугольника (гептаграммы): 7/2 и 7/3. Методы их построения аналогичны построению обычного семиугольника, только вершины нужно соединять через одну (7/2) или через две (7/3).

Правильный восьмиугольник

 

Правильный восьмиугольник

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой.

Свойства


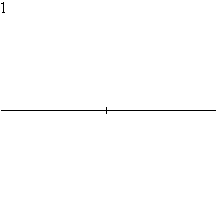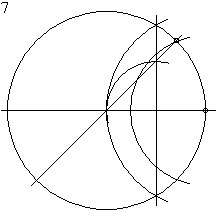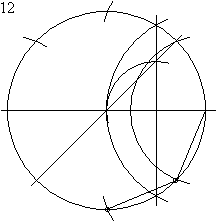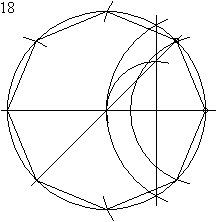
Построение правильного восьмиугольника

Восьмиугольник можно построить, проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080^°.
Угол правильного восьмиугольника составляет 135^°

Формулы расчёта параметров правильного восьмиугольника

Примем:
* t — длина стороны восьмиугольника
* r — радиус вписанной окружности
* R — радиус описанной окружности
* S — площадь восьмиугольника
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной 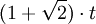, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:
* Радиус вписанной окружности правильного восьмиугольника:

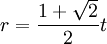
* Радиус описанной окружности правильного восьмиугольника:

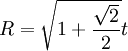
* Площадь правильного восьмиугольника:

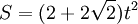
Правильный девятиугольник

 

Правильный девятиугольник

Правильный девятиугольник — это правильный многоугольник с девятью сторонами.
Свойства

Правильный девятиугольник имеет внутренние углы, равные 140^°. Площадь правильного девятиугольника со стороной A определяется выражением


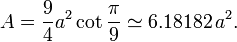
Построение

Хотя правильный девятиугольник и невозможно построить с помощью циркуля и линейки, существуют методы построения достаточно точных приближений.

Девятиугольные звёзды

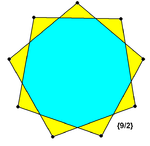
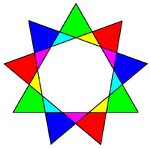
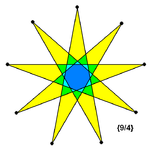
Существует три звёздчатых девятиугольника: {9/2}, {9/3} и {9/4}, причём звезда {9/3} состоит из трёх равносторонних треугольников:

Правильный семнадцатиугольник

 

Правильный семнадцатиугольник

Правильный семнадцатиугольник - геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности.
Свойства

Центральный угол a равен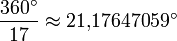
Отношение длины стороны к радиусу описанной окружности составляет

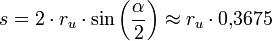
Правильный семнадцатиугольник можно построить при помощи циркуля и линейки, что было доказано Гауссом в 1796 году.

Факты

* Гаусс был настолько воодушевлён своим открытием, что в конце жизни завещал, чтобы правильный семнадцатиугольник высекли на его могиле. Скульптор отказался это сделать, утверждая, что построение будет настолько сложным, что результат нельзя будет отличить от окружности.
* В 1825 году Йоханнес Эрхингер впервые опубликовал подробное описание построения правильного семнадцатиугольника в 64 шагах. Ниже приводится это построение.

Примерное построение

1. Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
2. Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
3. Делим пополам отрезок EB (точка F).
4. строим перпендикуляр к AB в точке F.
* Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.
Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P₃ и P₁₄.
При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.

Построение семнадцатиугольника циркулем и линейкой в 64 шага по Йоханнесу Эрхингеру